Designing robotic swarms
Small robots have limited perception and processing power. This is an inconvenient truth that we have to deal with. With swarm intelligence, however, we can unlock their potential by enabling them to work together.
In this project, central to my PhD research, I set out to develop machine learning algorithms that would enable large teams of robots to collaborate together while verifying that their local choices would ultimately result in achieving the cooperative goal.
Developing a novel algorithm for emergent behavior
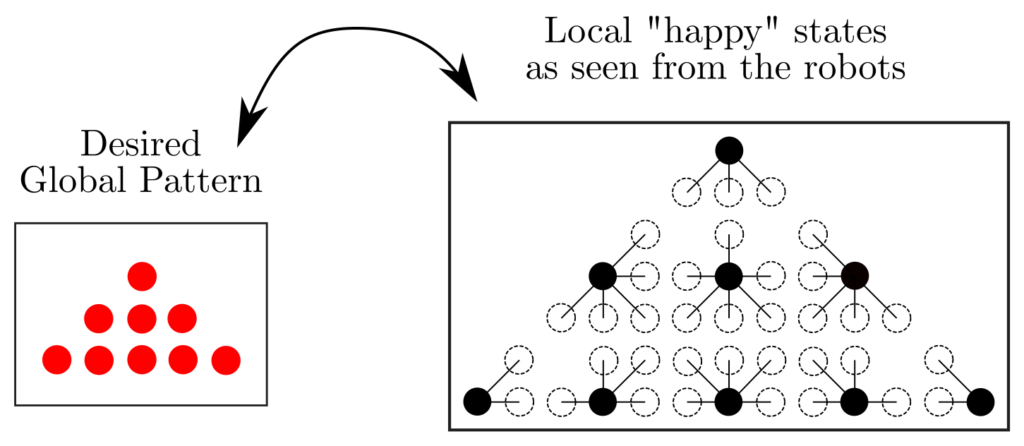
Prior to stepping into the machine learning domain, we needed to explore the complexity of swarms and understand the role of the single robot within the grand scheme. Pattern formation by very cognitively limited robots was chosen as a study case for this purpose. How limited were the robots? They were anonymous (no IDs!), without memory, reactive, homogeneous, could not communicate, could not plan ahead, no synchronization between their clocks, and had no global positioning (no GPS!). Essentially, they did not know anything except the current relative position of their closest neighbors and a knowledge of North. How, then, could we make them form patterns together?
Delving into such a restricted problems allowed us to explore what it means to solve a cooperative challenge from the perspective of the individual robot. This ultimately brought to the development of a novel algorithm to enable swarms of robots with limited knowledge and no communication to arrange into a larger pattern, which was then published in the journal Swarm Intelligence.The three rules of swarming
The algorithm followed three simple and bio-inspired rules:
- Be safe (avoid collisions)
- Be social (avoid moving away from peers)
- Be happy (stay in desired local states)
The first two rules allow the swarm to reshuffle freely while never separating in multiple groups or experiencing collisions. The third rule tells robots to remain in "happy" states, should they find themselves in one, else they need to move in search of "happiness". A "happy" state is a local state observations whereby the agent is "happy", and thus does not move. Unbeknownst to the robots (they are too cognitively limited), the global desired pattern is achieved once all robots are "happy". They form the pattern by self-organizing into the correct "puzzle-piece" that forms the "puzzle".
Additionally, the paper introduces a novel verification procedure to check whether the behavior of the robots is such that the swarm, as a whole, can eventually achieve its goal when starting from arbitrary initial conditions.
The novelty of this procedure is that it analyzes the local state and action space of an agent, meaning that we can verify a global property by a local inspection of the behavior of a single robot, rather than looking at the swarm as a whole.
Enough reading - you can see the algorithm in action in the video below!
Optimizing the behavior of swarms
The theory developed in the above provided us with a reliable method for "clueless" robots to arrange into larger patterns. Here, were were faced with two challenges:
- Optimizing the behavior of robots so that they would learn to become "happy" efficiently, without wasting time with random actions.
- Abstracting our ideas to cooperative tasks other than pattern formation.
PageRank centrality as a way to measure "happiness"
Our latest research provides a novel solution inspired by Google’s famous PageRank algorithm in order to evaluate a behavior without any simulation, but only based on a model of the local interactions that the agent experiences. The PageRank algorithm was developed by the founders of Google back in the late '90s. Its objective was to sort through webpages and find the popular ones. This was done by evaluating how likely it would be for a web surfer to arrive at a webpage when clicking hyperlinks. This algorithm gave Google a competitive advantage.
Just as a web surfer surfs the web, we thought to model the experiences of a robot "navigating" in the swarm. The states that the robot can be in become like websites to visit, and the actions that the robot can take become hyperlinks.
We then aimed for the machine learning algorithm (in this case, an evolutionary optimizer) to maximize the likelihood of robots to end up in "happy" states. This is a computationally efficient approach that requires no simulation. Because it only analyzes the behavior of a single robot, rather than the whole swarm, it allows to develop complex behaviors for larger swarms without the same scalability issues.
In addition to pattern formation, we also showed how to apply this to a consensus task (where the robots need to agree on a common objective) and an aggregation task (where the robots need to gather together). The algorithm was published here.